|
Les coefficients de forme ont une grande importance pour l’estimation du volume-bois sur pied des arbres et peuplements forestiers. Cette estimation devient rapide et aisée si pour chaque essence forestière est établie une table où sont rangées ces coefficients en fonction de la hauteur des arbres. Cette contribution propose une table des coefficients de forme du pin d’Alep et concerne un reboisement réalisé en 1890 dans la région de Tlemcen (Ouest d’Algérie). La méthode choisie pour son établissement n’exige pas l’abattage d’un grand nombre d’arbres (50 à 80 arbres seulement), et utilise la relation qui existe entre les coefficients naturels et les coefficients artificiels (à hauteur d’homme). Pratiquement, la table présente un double intérêt : connaître davantage les valeurs des coefficients de forme du pin d’Alep d’une part, et permettre le cubage rapide des arbres sur pied dans notre zone d’étude ou dans d’autres stations similaires.
I. INTRODUCTION
L’inventaire d’aménagement, mené classiquement par les forestiers aménagistes, consiste essentiellement en l’analyse descriptive et dendrométrique des peuplements forestiers. Il doit fournir les renseignements nécessaires pour la préparation des plans d’aménagement relativement intensifs de surfaces limitées. Il est destiné à estimer le volume bois sur pied et les potentialités des peuplements. L’estimation des volumes par essence doit se réaliser pour chaque peuplement individuel à l’intérieur de la forêt et les différentes stations doivent être reconnues. Il existe deux grandes catégories de méthodes pour estimer le volume des arbres sur pied : estimation directe par mesure du défilement et estimation indirecte par tarifs de cubage. Bien qu’elle soit coûteuse, la mesure directe du défilement est la plus exacte puisqu’elle prend en compte la forme réelle de la tige : Il est reconnu depuis longtemps que pour un diamètre et une hauteur donnée, le volume d’un arbre est intimement lié à sa forme (Hoyer, 1985, Ung, 1989).
Différentes expressions dendrométriques ont été établies pour matérialiser la forme générale de la tige d’un arbre, dont l’une couramment utilisée dans la pratique forestière, est le coefficient de forme (pardé et al 1988). Ce dernier est le rapport entre le volume de la tige de l’arbre jusqu’à une découpe fixée en grosseur ou en longueur, et le volume du cylindre ayant comme base la surface terrière g de la section à une hauteur fixée, et comme longueur, la hauteur hr (de référence) du volume considéré : fi = v/gihr (1). Lorsque le niveau « i » correspond à la hauteur d’homme (soit à 1.3 m du sol), on définit le coefficient de forme « à hauteur d’homme » ou « à hauteur de poitrine » ou le « coefficient artificiel de forme » selon les auteurs. L’inconvénient majeur de ce coefficient est sa dépendance de la hauteur. Les autres expressions mathématiques caractérisent la forme des tiges par une relation entre les diamètres mesurés à deux niveaux différents (M’hirit et al. 1985). Leur forme générale est la suivante (Ung, 1989) : d/dhp = f (h/H) (2) où d est le diamètre de la tige à la hauteur h, dhp le diamètre à hauteur de poitrine, et H la hauteur totale de l’arbre.
En dendrométrie sont connus d’autres coefficients de forme autres que celui mesuré à hauteur d’homme (1.30m). En 1880, Smallian et Pressler proposèrent les coefficients naturels de forme (Doukhovnikov, 1983) : Au début, le coefficient naturel de forme est défini par le rapport d’un volume-tige donné et le volume d’un cylindre ayant pour base la surface terrière à 1/20 de la hauteur de la tige, et pour hauteur la hauteur de la tige. Plus tard, cette notion est élargie, par la mesure des surfaces terrières à des hauteurs relatives quelconques (1/n). Il s’exprime par conséquent, par la formule : fn = v/g1/ nh (3). Le cas particulier du coefficient naturel est le coefficient de forme absolu qui se rapporte à la surface terrière mesurée à la base de la tige, autrement dit, à une hauteur relative 1/∞ = 0 ce qui donne f0 = v/g0 h (4).
Les trois types de coefficients de forme (f1.3 ; fn et f0) ont une grande importance pour le cubage des arbres et des peuplements. En effet, les équations basées sur la surface terrière, la hauteur dominante (ou moyenne), et une estimation de (f) permettent le calcul rapide du volume des peuplements. Mais les coefficients de forme sont difficilement appréciés ou mesurés avec précision pour un observateur non averti (Pardé, 1988). Bien qu’on peut les estimer à partir de tables de production ou mesurés avec le relascope de Bitterlicht, on les emploie aussi sous forme de tables dont la construction peut être réalisée par quatre méthodes : la méthode statistique, la méthode du coefficient de décroissance à hauteur d’homme, la méthode de la décroissance métrique et la méthode du coefficient naturel de forme à hauteur relative (0.x). L’inconvénient commun aux trois premières méthodes est qu’il faut abattre un grand nombre d’arbres échantillons (quelques milliers pour la méthode statistique par exemple).
La méthode des coefficients naturels, en utilisant la relation qui existe entre les coefficients artificiels à hauteur d’homme et ceux naturels, permet d’éviter les désavantages des autres méthodes. En effet, et contrairement aux premiers, le coefficient naturel est totalement indépendant de la hauteur de l’arbre et est l’expression réelle de sa forme. En outre, la méthode n’exige pas l’abattage d’un grand nombre d’arbres échantillons, et on peut se contenter de 60 à 80 arbres. Un autre avantage de la méthode est que les coefficients naturels obtenus sont considérés et utilisés dans la pratique comme artificiels. L’établissement d’une table des coefficients de forme du pin d’Alep (essence résineuse dominante en Algérie) aura donc un double intérêt : connaître les valeurs des coefficients de forme de pin d’Alep issu d’un reboisement, et permettre aux forestiers de surmonter les contraintes liées souvent, au cubage des arbres et des peuplements sur pied à cause de l’absence de tarifs de cubage et de tables de production.
II. PRESENTATION DE LA ZONE D’ETUDE
La forêt domaniale suburbaine de Tlemcen est un boisement pur de pin d’Alep (Pinus Halepensis. Mill) datant de 1890. Elle est localisée en amont de la ville de Tlemcen, à une altitude moyenne de 1023 m. Son sous bois est caractérisé par la présence du genévrier oxycédere (Juniperus oxycedrus), de l’asperge (Asparagus acutifolius), du doum (Ampelodesma mauritanica), du chêne vert (Quercus ilex), du genêt épineux (Calycotome spinosa) et du palmier nain (Chamaerops humilis). Généralement, elle présente une homogénéité topographique à l’exception de sa partie nord, où nous assistons à un changement de relief et où la pente est de 25% et plus. La forêt se développe sur du substrat calcaire sous l’influence de climat méditerranéen, avec deux saisons bien tranchées : Une saison hivernale froide et humide de courte durée, et une saison estivale chaude et sèche de longue durée (Bouazza, 1991).
 Figure 1 : Localisation de la région et la zone d’étude. (Quadrillage kilométrique Lambert- Nord Algérie)
III. MATERIEL ET METHODES
3.1. Principe de la méthode
C’est une méthode qui combine les avantages des coefficients artificiels et naturels : les coefficients sont calculés comme naturels, mais en pratique s’utilisent comme artificiels. Une telle décision s’est basée sur la relation qui existe entre les deux types de coefficients. En effet pour une série de coefficients naturels, il y aura certainement un, qui sera en même temps artificiel et naturel : c’est celui qui correspond à la hauteur relative 1.3/h. La figure 2 montre que pour une tige donnée, on peut calculer plusieurs coefficients naturels de forme. La tige est découpée en cinq sections et comme base de calcul sont utilisées les surfaces terrières (diamètres) mesurées à 1/10 (0.1), 3/10 (0.3), 5/10 (0.5), 7/10 (0.7) et 9/10 (0.9) de la hauteur. On remarque que plus haut est mesurée le diamètre, plus petit sera le volume du cylindre qu’on doit comparer au volume de la tige. Ceci conduit à des valeurs de plus en plus grandes des coefficients naturels lui correspondant.
 Figure 2 : Schéma de Segmentation de la tige en billons d’égale longueur
Figure 3 : courbe des coefficients naturels de forme
Graphiquement, ces coefficients naturels sont exprimés par la courbe des coefficients naturels de forme (figure 3) à partir de laquelle, on peut déterminer les coefficients de forme à hauteur d’homme (f1.3). En fait, ce dernier est un coefficient naturel à hauteur relative 1.3/h. Par conséquent, il représente toujours un point de la courbe et ceci confirme cette relation qui existe entre les coefficients naturels (fn) et artificiels à hauteur d’homme (f1.3). Pour établir des tables de coef de forme par cette méthode, quatre étapes sont nécessaires :
 Sélectionner et traiter un nombre suffisant d’arbres Sélectionner et traiter un nombre suffisant d’arbres
 Calculer pour chaque arbre modèle une série de coefficients naturels Calculer pour chaque arbre modèle une série de coefficients naturels
 Calculer la courbe moyenne arithmétique des coefficients naturels Calculer la courbe moyenne arithmétique des coefficients naturels
 Construire la table des coef. naturels de forme. Construire la table des coef. naturels de forme.
La méthode exige généralement l’abattage et la mesure d’une soixantaine d’arbres modèles d’une hauteur supérieure à 20 mètres. Les mesures prises sur les arbres modèles sont les mêmes que celles qui servent au cubage des arbres par billons successifs, et auxquels est appliqué la formule commerciale de Huber. Le profil de chaque arbre modèle est ensuite tracé dans un système de coordonnées, avec en ordonnées les diamètres, et en abscisses les hauteurs auxquelles sont mesurées ces diamètres. Pour chaque arbre modèle traité de cette façon, seront calculés une série de coefficients naturels de forme. A partir de ces derniers, sera calculée graphiquement la courbe moyenne d’où seront lus directement les coefficients naturels à hauteur relative (1.3/h), correspondant à différentes valeurs de la hauteur.
3.2. Mesures terrain
Les données recueillies concernent la description du peuplement étudié et les caractéristiques dendrométriques des arbres.
3.2.1. Description du peuplement
La description de certaines variables qualitatives permet d’obtenir une caractérisation de la station rendant possible sa comparaison avec d’autres stations. En effet, le problème fondamental du cubage des arbres sur pied concerne la relation entre la forme de l’arbre et la station (Ung C-H, 2006). Généralement, la description doit porter sur la composition, le couvert, les difficultés physiques d’exploitation et l’importance relative de la régénération des différentes espèces. Cette description est complétée par un relevé écologique permettant entre autres de déterminer la série évolutive du peuplement (Saucier 1992). Dans notre cas, quatre variables ont été décrites : l’exposition et la pente (avec un clisimétre-boussole), l’altitude (avec un altimètre), la pente, le sol, et enfin le recouvrement de la strate arborée. Le tableau 1 résume les caractéristiques de la zone d’étude par placette.
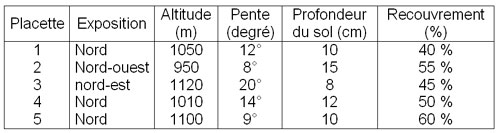 Tableau 1 : Caractéristiques stationnelles des placettes d’études
3.2.2 Mesure des caractéristiques dendrométriques des arbres
Les deux paramètres dendrométriques nécessaires à notre étude sont le diamètre et la hauteur. L’abattage des arbres étant impossible, on a utilisé le relascope de Bitterlich puisque cet instrument permet de mesurer les diamètres à différentes hauteurs. Dans chacune des 5 placettes, 10 arbres modèles ont été sélectionnés, soit 50 arbres au total. Les critères de sélection sont la rectitude du fût, la hauteur, et l’état sanitaire. Deux procédés sont à choisir pour la prise des mesures : découper la tige en plusieurs tronces successives d’égale longueur (2m par exemple) et dans ce cas le diamètre au milieu de la première sera mesuré à 1 m de hauteur, celui de la deuxième à 3 m et ainsi de suite. Ou bien découper la tige en un nombre défini de tronces (soit 10 dans notre cas) mais de longueur variable en fonction de la hauteur totale de l’arbre.
IV. RESULTATS ET DISCUSSION
Pour un arbre modèle donné, on doit calculer une série de coefficients naturels par la formule fn=gn/g0,x (5) où gn est la surface terrière naturelle de l’arbre : C’est la moyenne arithmétique des surfaces terrières mesurées au milieu de chaque billon. Etant donné que les arbres ont été divisés en 10 billons (soit 20 demi - billons), le milieu du premier billon sera à 1/20 de la hauteur de l’arbre, celui du deuxième à 3/20, du troisième à 5/20, du quatrième à 7/20 etc. Autrement dit, on obtient les hauteurs relatives 0.05 ; 0.150 ; 0.250 ; 0.350 etc. Mais Il faut toujours prendre en compte la hauteur relative 0.x= 0.100. Ayant calculé gn et g0.x, on peut facilement déterminer pour l’arbre modèle donné, les coef naturels de forme par la formule (5). Le tableau 1 montre un exemple parmi les 50 arbres traités dans cette étude.
Tableau 2 : Exemple de Calcul des coefficients naturels de forme de l’arbre modèle n°2
De la même façon, sont calculés les coefficients de forme pour les 49 autres arbres modèles, en établissant pour chacun d’eux un tableau similaire au tableau 1. La suite du travail consiste à construire le tableau 2 où sont donnés pour les 50 arbres, les coefficients correspondant aux hauteurs relatives de 0.05 à 0.250 puisque ceux se rapportant à de grandes hauteurs relatives ne sont pas nécessaires. Les coefficients sont additionnés par hauteur relative puis divisés par le nombre d’arbres (soit 50). De cette façon, on obtient une série moyenne de coefficients naturels de forme.
Tableau 3 : Valeurs des coefficients naturels de forme des différents arbres modèles
Graphiquement, cette série est illustrée par la figure 2 qui représente la courbe moyenne des coefficients de forme du pin d’Alep et qui permet aisément de construire la table correspondante. Mais encore faut-il connaître cet intervalle dans lequel se situent les hauteurs des arbres qui feront l’objet d’un cubage au moyen de cette table. Ensuite, la hauteur absolue à hauteur d’homme (1.3 m) est convertie en hauteur relative en la divisant par la hauteur de l’arbre. A partir de la courbe des coefficients de forme (fig. 2), sont lus puis rangés dans une table (voir table n°3), les coef naturels pour des hauteurs relatives 1.3/h. Ces derniers seront utilisés comme s’ils étaient mesurés à hauteur d’homme (soit à 1.3m).
Figure 4 : Courbe moyenne des coefficients naturels de forme
Tableau 4 : Table des coefficients naturels de forme du pin d’Alep issu d’un reboisement. Région de Tlemcen - Ouest Algérien
Les valeurs obtenues nous donnent une première idée sur les valeurs que peut prendre le coefficient de forme du pin d’Alep issu d’un reboisement en fonction de sa hauteur. Ces valeurs ne s’éloignent pas beaucoup de ceux obtenus dans d’autres régions. A titre de comparaison, le tableau n°4 donne les valeurs obtenues pour le pin d’Alep naturel dans la région de l’Aures (Est algérien) en fonction de la hauteur dominante.
Tableau 5 : Valeurs des coefficients de forme en fonction de la hauteur dominante. Région de l’Aures. Est algérien (Bentouati, 2006)
Pratiquement et pour des agents forestiers non expérimentés, ou ayant des difficultés à utiliser les instruments optiques tel que le relascope de Bitterlich, cette table (voir Tableau 4) leur sera d’une grande utilité pour le cubage rapide des arbres sur pied. Il leur suffit d’utiliser la formule V=GHF. La surface terrière (G) est calculée en fonction du diamètre mesuré à 1.3m, la hauteur (H) est mesurée avec un dendrométre blume-leiss et F, lu directement de la table 3 en fonction de la hauteur de l’arbre. Cette formule est aussi valable pour l’estimation du volume moyen par hectare des peuplements de pin d’Alep si la surface terrière par hectare est déterminée par le relascope de Bitterlich. Dans ce cas la hauteur H sera la hauteur moyenne (ou dominante) du peuplement et F, le coef de forme moyen lui correspondant.
En ce qui concerne la précision de cette table, trois types d’erreurs sont à craindre : erreur liée à la lecture de l’instrument, erreur liée à l’opérateur, erreur liée à l’instrument utilisé. Pour le moment et en l’absence de données de référence, les trois erreurs précitées ne peuvent être déterminées. Ces erreurs pourraient être accentuées par les conditions stationnelles : terrain rocheux et accidenté, ou sylvicoles : mauvais élagage, qui ne permettent pas toujours une utilisation aisée du relascope. C’est ce qui nous a contraint de fournir de grands efforts et manifester une grande patience pour la mesure des 50 arbres modèles.
V. CONCLUSION
La table des coefficients de forme établie sera certainement d’une grande utilité pour les inventaires d’aménagement des forêts de pin d’Alep dans la région, et particulièrement ceux issus de reboisement. Le temps et les efforts fournis pour sa construction seront économisés par les agents forestiers pour l’estimation du volume sur pied des peuplements de pin d’Alep dans la région. D’autre part, la méthode des coefficients naturels de forme qui n’exige pas l’abattage d’un grand nombre d’arbres, peut être utilisé pour d’autres essences (résineux ou feuillus). Les tables qui en résultent serviront ultérieurement à la construction de tarifs de cubage. Toutefois, et afin d’améliorer l’estimation du volume sur pied, il est recommandé d’acquérir davantage de connaissances sur la relation de la forme du pin d’Alep avec la station.
Références
BENTOUATI A., 2006. Croissance, productivité et aménagement des forêts de pin d’Alep. M) du massif de Ouled Yagoub (Khenchela-Aures). Thèse de doctorat d’état en Sci.Agron. Université El Hadj Lakhdar, Batna, Algérie. 116p.
BOUAZZA. M., 1991. Etude phyto-écologique de la steppe à stipa tenacissima au sud de Sebdou - Oranie- Algérie).Thèse en sciences, Fac.Sc. Marseille- Saint - Jérôme, 1991, 109p.
DOUKHOVNIKOV.J et MIKHOV.I., 1982. Dendrométrie. Ed.zemisdat, Sofia, Bulgarie.220p.
HOYER.G. E., 1985. Tree form quotients as variables in volume estimation. Res. Pap. PNW-345. Portland, OR : U.S. Department of Agriculture, Forest Service, Pacific Northwest Forest and Range Experiment Station ; 1985. 16p.
M’HIRIT.O et POSTAIRE.J.G., 1984, Analyse de la forme des tiges pour la construction de tarifs de cubage. Application au cèdre du Maroc (Cedrus atlantica. Manetti). Ann.sc.for.41 (3). 303-322.
PARDÉ, J. ET J. BOUCHON., 1988, Dendrométrie. 2e édition. Ecole nationale du génie rural, des eaux et forêts. France, 328 p.
SAUCIER, J.-P. 1992. Croissance et rendement en fonction des types écologiques photointerprétés dans la région écologique 5a-Basses et Moyennes Appalaches (Québec). Thèse de maîtrise. Faculté de foresterie et de géomatique, Université Laval. 202 p.
UNG.C-H, 1989. Forme des tiges d’érable à sucre et de hêtre à grandes feuilles dans une jeune futaie selon leur position sociale et leur âge. Ann.Sci.For. 46(3),261-271.
UNG.C-H., 2006. Inventaire par échantillonnage pour estimer la production ligneuse et son accroissement. Partie 3. Acquisition et traitement des informations. Cours n°25.Formation continue. Ed. Ordre des ingénieurs forestiers du Québec.19p.
Presentation de l’auteur :
 Ingénieur d’état forestier, option : aménagement forestier, 42 ans, Diplômé en 1990 de l’institut supérieur des sciences forestières, Sofia, Bulgarie. Ingénieur d’état forestier, option : aménagement forestier, 42 ans, Diplômé en 1990 de l’institut supérieur des sciences forestières, Sofia, Bulgarie.
 Diplôme de Magistère en foresterie, obtenu en 2002 à l’université de Tlemcen Diplôme de Magistère en foresterie, obtenu en 2002 à l’université de Tlemcen
 Formateur de 1991 à 1995 et de 1996 à1998, respectivement au centre de formation des adjoints techniques forestiers (Sidi Bel-abbes) et au centre national de perfectionnement en foresterie (Tlemcen) où j’ai enseigné l’aménagement forestier et la dendrométrie. Formateur de 1991 à 1995 et de 1996 à1998, respectivement au centre de formation des adjoints techniques forestiers (Sidi Bel-abbes) et au centre national de perfectionnement en foresterie (Tlemcen) où j’ai enseigné l’aménagement forestier et la dendrométrie.
 Depuis 1998, je suis chargé du cours d’aménagement forestier au département de foresterie, l’université de Tlemcen, Algérie.
Je travaille actuellement sur l’apport de la télédétection satellite pour l’aménagement forestier en zones semi-arides de l’ouest algérien, et particulièrement sur la cartographie forestière et l’estimation des potentialités de production. Depuis 1998, je suis chargé du cours d’aménagement forestier au département de foresterie, l’université de Tlemcen, Algérie.
Je travaille actuellement sur l’apport de la télédétection satellite pour l’aménagement forestier en zones semi-arides de l’ouest algérien, et particulièrement sur la cartographie forestière et l’estimation des potentialités de production.
Kada Bencherif
|
 ii
ii
 ii
ii